CTI-VQA [知识蒸馏]
文章简介
传统的VQA模型分为两类,一类是自由形式回答的Free-Form Opened-Ended(FFOE),另一类是多选题Multiple Choice(MC)
两种VQA任务的传统方法主要是学习图像和问题的联合表示,而对答案的处理都是”被动”的,即只将答案视为分类目标,但是一个答案与其对应的问题图像输入具有很高的相关性,因此,从这三个输入中联合而明确地提取信息将会给出一个非常有价值的联合表示,因此作者在这篇文章中提出了一种新的三线性交互模型,以学习三种输入(图片,问题,答案)之间的高水平的关联
三线性交互的主要难点是维数问题,计算量大,内存需求大,为了解决这个问题,作者提出了利用PARALIND分解将一个大张量分解为小张量,从而减少了计算量和内存的使用
FFOE VQA中的答案信息只在训练阶段提供,在测试阶段不提供,为了将三线性交互应用于FFOE VQA中,作者提出利用知识蒸馏将三线性模型转化为双线性模型,提取的双线性模型只需要对图像和问题作为输入,因此可以用于测试阶段,而对于MC VQA,则可以直接利用三线性模型,作者在TDIUC,VQA-2.0和Visual7W上都取得了SOTA的结果
文章的主要贡献如下:
- 提出了一种新的三线性交互模型,该模型能同时学习图像、问题和回答信息在VQA任务中的高水平联合表示
- 利用PARALIND分解来处理三线性相互作用中的维数问题
- 为了使提出的三线性交互适用于FFOE VQA,提出利用知识蒸馏将知识从三线性交互模型转移到双线性交互模型
相关工作
VQA中的联合嵌入
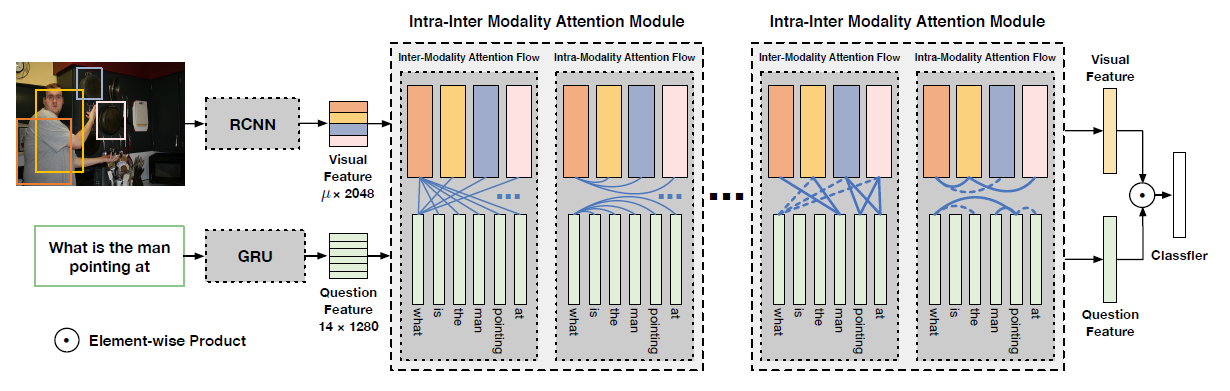
在SOTA的VQA算法中,输入图像和问题的特征通常用矩阵形式表示。例如,每幅图像由若干感兴趣的区域描述,每个区域由一个特征向量表示,类似的思想也适用于问题,例如,一个问题包含若干个单词,每个单词用一个特征向量表示,一个图像区域和一个单词之间充分表达的交互作用应该是它们两个对应向量之间的外积,外积允许两个向量的所有元素之间的乘法相互作用,然而,在每一对可能的区域和单词之间使用外积完全双线性交互将极大地增加输出空间,大部分研究都试图压缩或分解完全双线性相互作用,而不是直接用外积计算完全双线性交互
不同于之前的学习双模态的联合表示或使用点积来简化三模态交互的研究,作者提出了一个三线性交互模型来同时学习三种模态的联合表征,首先推导了三种模态见的完全三线性相互作用,然后采用分解方法为交互产生一个紧凑的模型(compact model)
知识蒸馏
在FFOE VQA中,以图像、问题和答案为输入的三线性交互模型只能用于训练阶段,而不能用于测试阶段,因为测试阶段没有答案,因此作者采用知识蒸馏的方式从三线性模型中将知识转移到双线性模型
主要灵感来源于Hinton’s seminar work
解读可见:https://zhuanlan.zhihu.com/p/24894102
紧凑三线性交互
完全三线性交互
设$M={M_1,M_2,M_3}$为三种输入,$M_t \in R^{n_t \times d_t}$,其中$n_t$是通道数,$d_t$是每个通道的维数,完全参数化三线性交互的结果为

$\tau$是一个可学习的张量,$vec(M_t)$是$M_t$的向量化,输出一个行向量,$\times_i$表示i-mode张量积
tensor $\tau$通过i-mode乘积学习了三个输入之间的相互作用,然而学习如此大的一个张量是不可行的,因此有必要减少$\tau$的大小
作者采用了unitary attention机制,令$z_p$表示通道的第p个三元组,每个三元组中的通道来自不同的输入,记每个通道在三元组中表示为$m_{1_i}$,$m_{2_j}$,$m_{3_k}$,那么z的完全参数化三线性交互结果为

依据unitary attention,z的近似可以表示为

作者计算了所有可能的三元组的加权和,第p个三元组和离散权值$M_p$相关,$M_p$集合即注意力图M,其计算方式如下

最终联合表示z可以被写为

参数分解
虽然三线性相互作用模型的大张量T被两个较小的张量$T_M$和$T_{sc}$所取代,但这两个张量的维数仍然很大,给学习带来很大困难,为了进一步降低计算的复杂度,对$T_M$和$T_{sc}$采用了PARALIND分解

R是切割参数,在分解率(直接与使用内存和计算成本相关)和性能之间建立平衡,$G_r$是一个学习的小张量,称为Tucker tensor,它的数量等于R,R的最大值一般设置为d1,d2,d3中的最大值,实验设置R=32,下图展示了PARALIND算法对Tm的分解

所以PARALIND分解可以被表示为

代入注意力图的计算式子得到

对Tsc的分解和Tm类似,这里设置切割参数R=1,Tsc最终可以表达为:

$z_T$的计算式子可以被重写为

因为$G_{sc}$秩为1,所以可以用点积近似计算

紧凑三线性交互用于VQA
对于VQA来说,其attention map可以表示为

联合表示被计算为

MC VQA
首先输入的问题和答案被裁剪到最大12个单词,空缺位置用0填充,之后每个单词都被嵌入一个300-D的GloVe word embedding来表示,每张图片被表示为$14\times14\times2048$的网格特征,从在ImageNet上预训练的ResNet-152的倒数第二层提取

样本输入被分为正样本和负样本,正样本标记为1,负样本标记为0,然后将这些样本通过CTI得到联合表示z,将联合表示通过二值分类器进行预测。利用二元交叉熵损失对模型进行训练
FFOE VQA
FFOE VQA需要将问题看出在一组预定义的答案上的分类问题,因此,每个问题-图像对的可能答案集合比MC VQA的情况下要多,对于每个问题图像输入,模型从其答案列表中获取所有可能的答案来计算联合表示,这将导致很高的计算成本,CTI在输入的时候要求V-Q-A,而在测试的时候是没有A的,因此作者对模型进行了改进,引入了知识蒸馏,模型如下

teacher model用V-Q-A作为输入,得到联合表示,然后将联合表示传入分类器,损失采用交叉熵,student model作者采用BAN2和SAN,用V-Q作为输入,将答案预测作为一个分类问题,损失函数定义为

$L_{CE}$是交叉熵损失,$Q_s$是student model标准的softmax输出,$y_{true}$是GT答案标签,$\alpha$是用来调整各部分loss重要性的超参数,$Q_S^\tau$,$Q_T^\tau$是采用了相同温度的student和teacher的softmax输出,计算方法为

对于教师模型和学生模型,logit $l$是相应分类器输出的预测
实验结果
消融实验

不同问题种类上的表现

attention map可视化

在TDIUC上和SOTA的比较