Learning To Count [VQA计数]

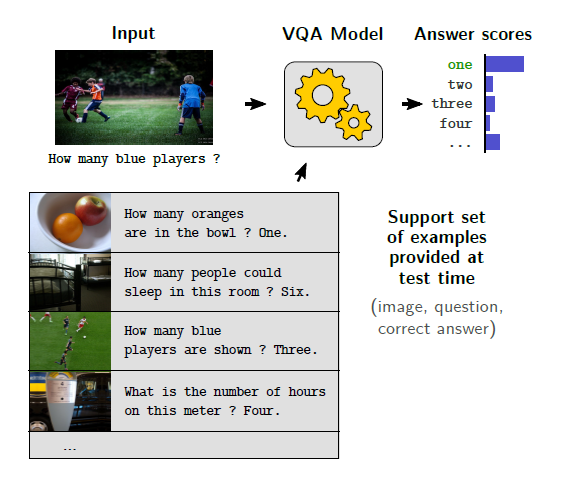
想要统计图中有几只猫通常需要这样几个步骤：理解实例的视觉表现，在图中找到实例以及计数

这在VQA中是一个常见的Task，然而目前的VQA系统在数据集bias之外的情况很难回答计数问题，主要原因是广泛使用的软注意力机制以及VQA中的计数并不像标准计数对计数目标有GT标定

模型需要能够对大量对象进行计数，并且在理想情况下，在非计数问题上的性能不受到损害，因此非常具有挑战性

为了简化这个task，作者采用object proposals，即将目标检测得到的bounding box和对应的对象特征作为输入而非从pixel层面学习。在复杂的场景中，通常会遇到重复计算重叠对象的问题，这是一个存在于许多自然图像中的问题，它会导致在真实场景中不准确的计数

文章的主要贡献是提出了一个可微的神经网络组件来完成计数，该组件与注意机制一起使用，避免了软注意的基本限制，同时产生强大的计数功能，实验表明，使用计数组件的相对简单的基线模型优于所有以前的模型，而不会降低其他类别的性能

greedy non-maximum suppression(NMS)通常用于消除重复的bounding box，使用它作为模型的一部分会出现的主要问题是它的梯度是分段常数，作者提出的模型不需要对保留哪些边框做出离散的决定，它输出计数特性，而不是更小的边框集，该组件可以很容易地集成到标准的VQA模型中去

对于VQA v2数据集，只有少数工作在计数问题上取得进展，Anderson et al.主要通过在视觉处理管道中使用了对象建议(object proposals)提高了精度，他们的对象建议网络是用单数和复数形式的类进行训练的，比如tree和trees不同，它只允许原始计数信息出现在ROI池化之后的对象特性中。而文中的模型使用object proposals上的attention map中出现的信息来创建计数特征，这样做的好处是，注意机制能够区分出任何东西，而不仅仅是属于具有复数形式的预定类别的对象

Trott et al.采用强化学习的Loss在训练集VQA v2和Visual Genome上训练了一个连续计数方法，他们的准确率得到了小幅的提高，但是不确定他们的方法能否集成了一半的VQA模型中，因为其loss函数不适用于非计数问题，他们在自己的数据集上进行评估，结果很难与VQA中现有的结果进行比较

Santoro et al.和Perez et al.在不采用bounding box和计数对象位置监督的情况下能够在synthetic CLEVR数据集中计数

Cohen et al.利用卷积接受域的重叠来提高计数性能，Chattopadhyay et al.将图像分割成较小的不重叠的块，每个块单独计数，最后合并在一起

在这两种情况下，卷积接收域(convolutional receptive fields)或块可以看作是一组定位结构固定的bounding box

PROBLEMS WITH SOFT ATTENTION

这一章节的核心观点是利用注意力机制得到的特征向量不足以支撑计数，需要采用attention maps

VQA模型一直受益于用前层卷积网络实现的图像中的软注意力(soft attention)，它学习输出feature map中每个空间位置的feature vector的权值，首先对权值进行归一化，然后对空间位置进行加权和，得到一个单独的feature vector，然而，软空间注意严重限制了模型的计数能力

考虑两个统计猫的数量的Task：一个是将猫的图像放在一个干净的背景之下，另一个由第一幅图像的两个并排副本组成，这里描述的对象既适用于spatial feature maps，也适用于object proposals作为输入

利用目标检测网络，在第一幅图像中可以检测到一只猫，在第二幅图像中检测到两只猫，三种检测结果都产生相同的特征向量，然后，注意力机制给同一只猫的三个实例分配相同的权重

attention机制常用的归一化方法softmax将权值和归一化为1，问题就出现在了这里，第一幅图中的猫得到了1的权值，第二幅图中的两只猫分别得到了0.5的权值，经过加权和后，第二幅图像中的两只猫被平均为一只猫，加权和后得到的特征向量在两幅图像之间是完全相同的，使用注意机制得到特征向量导致丢失了attention map中可能的计数信息，所有将权重和归一化为1的方法都会遇到这样的问题

Multiple glimpses以及several steps of attention都无法解决这个问题，每个glimpse或step都不能单独将一个对象分离出来，因为给一个特征向量的注意权值不依赖于其他被关注的特征向量

Hard attention和structured attention是这个问题的可能解法，尽管到目前为止没有发现后者的计数能力有显著提高

Ren & Zemel限制注意力一次只在一个bounding box内work来避免这个问题，这和作者提出的用object proposal来计数有异曲同工之妙

如果不将权重归一化，则输出特征的尺度取决于检测到的对象的数量，在有10只猫的图像中，输出的特征向量按比例增加到10。深度神经网络对尺寸是非常敏感的(scale-sensitive)，权重的初始化和激活的规模非常重要，特征尺度的增加会使得分类器不得不学习与计数相关的联合特征，这对计数问题来说并不合理。Teney et al.实验证明了sigmoid归一化不仅会略微降低非数字问题的准确性，而且对计数也没有帮助

COUNTING COMPONENT

处理重叠object proposals的核心思想是将这些object proposals转换成基于它们如何重叠的图表，然后以特定的方式去除和缩放边缘，从而恢复对底层对象数量的估计

总体策略是，主要针对完全重叠或完全不同的完美注意力映射和边框这种不现实的极端情况来设计组件

作者提出的组件在能够提升计数的同时仍然允许模型使用软注意力

INPUT

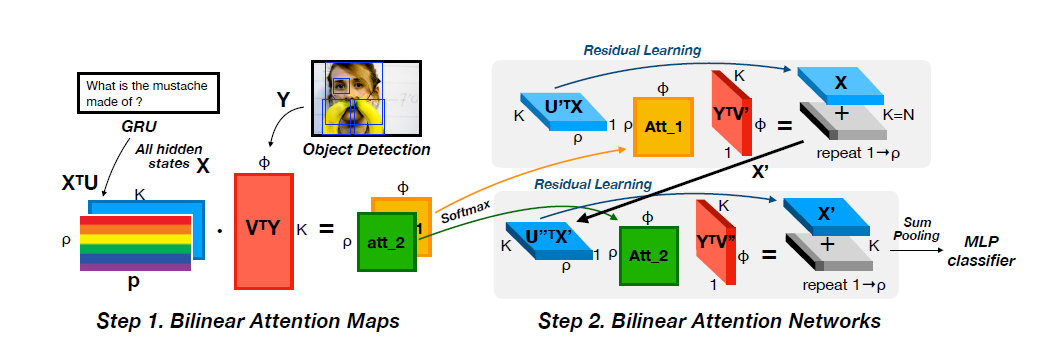
给定object proposals的feature，注意力机制根据问题对每个proposal设定权重，计数组件以最大的n个注意力权重$a=[a_1,\dots,a_n]^T$和对应的bounding box $b=[b_1,\dots,b_n]^T$作为输入

DEDUPLICATION

首先将注意力权重向量a转换为更容易利用边界框的图形表示，因此计算注意权值的外积(叉乘)，得到注意矩阵

$A=aa^T$

A可以看做一个加权有向图的邻接矩阵，第i个点表示与$a_i$相关的object proposal，连接i和j的边权重为$a_i*a_j$，若$a_i$值只有0/1，那么外积就等价于逻辑与，所以只包含满足$a_i = 1$的顶点的子图是一个有自环的有向完全图

作者想要做的是在这张图上消除边，带自环的有向完全图的边和点的关系是$|E|=|V|^2$，$|E|$可以通过对邻接矩阵中的项求和来计算，$|V|$就是计数的答案

$\sqrt{|E|}=\sum_ia_i$

当所有proposal都完全不同时，组件可以输出与默认情况下简单地对原始注意权重求和相同的结果

为了实现目标，需要消除两种类型的边：对象内的边和对象间的边

INTRA-OBJECT EDGES

首先消除单个对象内部重复proposals之间的边

作者采用通常的IoU方法来比较两个bounding box，距离矩阵D定义为

$D_{ij}=1-IoU(b_i,b_j)$

D也可以被看成一个邻接矩阵，除了重叠的bounding box之外两两之间都有边，通过注意矩阵和距离矩阵的矩阵元素相乘来删除对象内部的边缘

$\bar{A}=f_1(A)\odot f_2(D)$

注意到$\bar{A}$不再有自环，为了使得$|E|=|V|^2$，需要再之后的处理中将自环加回去

INTER-OBJECT EDGES

然后消除对象间因重复proposal导致的边

核心思想是计算与每个独立对象相关的proposal的数量，然后按该数字按比例缩小其关联边的权值

如果一个对象有两个proposal，那么这些proposal的相连的边应按0.5的比例缩放，本质上这是对每个底层对象计算proposals的平均值，因为只使用边权的总和来计算最后的计数答案，由于不知道有多少个proposal是属于这个对象的，所以需要估算，作者采用相同对象的proposal是相似的这个GT来实现这一点

注意到$\bar{A}$没有自环，且在属于同一个对象的两个proposal之间没有没有边，因此两个非零行在$\bar{A}$中相等当且仅当两个proposal相同。因此在比较行的时候需要一个相似度函数，当全相同时返回1，存在至少一个位置不同时返回0，对于proposal相似度函数为